지난 포스팅에서는 Google Earth Engine(GEE)에서 받은 Sentienl-1 위성 자료를 읽고 가시화 하는 방법을 설명했다.
이번 포스팅에서는 읽어온 위성영상의 통계적 특성을 분석하는 방법에 대해서 설명할 것이다.
지난 번에 받은 자료를 열어보면 다음과 같다.
plt.imshow(data['Band'], cmap='gray')
plt.title(data['Product Name'])
plt.clim(0,1)
plt.show()
이미지 슬라이싱
통계적을 분석을 한다는 것은 데이터의 일부를 통해 전체의 특성을 분석하는 의미다.
따라서, 통계적 분석 이전에 영상의 일부를 잘라내는 작업을 수행한다. 이를 파이썬에서는 슬라이싱이라고 한다.
인천 국제공항은 y축과 x축으로 각각 0~1250, 250~1250 정도에 위치해있다.
그리고, 송도 지역은 1500~마지막, 1750~2750 정도에 위치해있다. 이 정보들을 이용해 해당 지역을 잘라 가시화해보면 다음과 같다.
plt.subplot(1,2,1)
sample = data['Band'][0:1250,250:1250]
plt.imshow(sample, cmap='gray')
plt.title('Inchein International Airport')
plt.clim(0,1)
plt.subplot(1,2,2)
sample = data['Band'][1500::,1750:2750]
plt.imshow(sample, cmap='gray')
plt.title('Songdo')
plt.clim(0,1)
plt.show()
이처럼 plt.subplot()을 이용하면 여러가지 그림을 한 번에 시각화할 수 있다.
그리고, 파이썬의 인덱스는 0부터 시작하기때문에 첫번째 픽셀의 위치는 0이고, 마지막 픽셀의 위치를 모를 때는
sample = data['Band'][1500::,1750:2750]에서와 같이 ::을 이용하면 된다.
정확한 값이 알고 싶으면 np.shape()를 이용하거나 영상의 메타데이터를 확인할 수 있다.
print(np.shape(data['Band']))
print(data['Meta Data']['height'], data['Meta Data']['width'])(2460, 3025)
2460 3025
통계분포 모델링
인공위성 자료를 이용하여 해양환경에서 선박을 탐지하기 위해서는 해양에 의한 픽셀과 선박에 의한 픽셀을 통계적으로 구분해야한다.
통계적으로 두 픽셀을 분류하는 방법은 우리가 잘 알고있는 데이터의 통계적 분포를 추정하고 임의의 픽셀을 비교해서 우리가 추정한 분포에 있는 픽셀인지 아닌지를 확인하는 것이다.
간단하게 말하면, 해수 픽셀은 대부분 0~0.1의 값을 갖는다고 가정했을 때 어떤 픽셀이 0.8의 값을 보인다면 확실하게 어떤 물체인지는 몰라도 해수는 아닐 것이라고 예상할 수 있다.
위성 영상을 분석할 때는 이러한 방법을 이용하고, 이러한 방법을 통계적 가설검정(Statistical Hypothesis Testing)이라고한다.
통계적 가설검정을 수행하기 위해서는 우리가 찾고자 하는 선박이 아닌 우리가 잘 알고 있는, 만연해있는 해수의 픽셀이 어떤 통계분포를 따르는지 알아야한다.
따라서, 해양지역의 일부를 다음과 같이 샘플링한다.
sample = data['Band'][2100::,0:400]
plt.imshow(sample, cmap='gray')
plt.title('Ocean Sample Area')
plt.clim(0,1)
plt.show()
SAR 영상의 특성상 해양지역이 굉장히 어둡게 보이지만 값이 없는 것은 아니다.
획득된 샘플을 히스토그램을 통해 분석하면 픽셀값이 어떤 분포를 보이는지 추정할 수 있다.
x,y = np.shape(sample)
bin = np.linspace(0,0.1,200)
a = plt.hist(sample.reshape(x*y),bin)
plt.title('Histogram')
plt.ylabel('Frequency')
plt.xlabel('Sigma_naught')
plt.show()
위의 히스토그램은 y축이 도수(빈도), x축이 후방산란계수(Backscattering Coefficient)를 나타낸다. 앞서 획득한 샘플에서 각각의 픽셀값을 갖는 픽셀이 몇개가 있는지를 나타낸 그래프다.
그런데, 통계적 가설검정을 이용하려면 히스토그램이 아닌 확률밀도함수(Probability Density Function, PDF)를 알아야한다.
하지만, PDF는 연속함수인데 컴퓨터의 연산 방법은 이산적이기 때문에 PDF를 추정하는 것은 사실상 불가능하다.
따라서, 히스토그램의 y축을 도수가 아닌 상대도수를 표현하고 x축의 샘플링 간격을 충분히 좁혀 PDF에 근사한 값을 이용한다.
다음과 같이 PDF에 근사한 그래프를 추정할 수 있다.
x = a[1][1::]
y = a[0]/sum(a[0])
plt.plot(x,y,'.')
plt.title('Estimated PDF')
plt.ylabel('Probability')
plt.xlabel('Sigma_naught')
plt.grid('on')
plt.show()
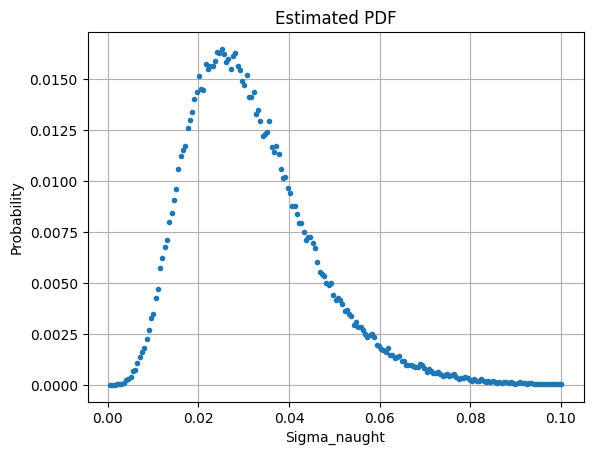
통계분포에도 저마다의 이름이 있다. 가장 유명한 모델이 가우스분포(Gaussian Distribution)다.
흔히, 정규분포라고 알려진 가우스분포는 평균값을 중심으로 대칭적인 분포를 보인다. 하지만, 앞서 구한 히스토그램에서도 알 수 있듯이 SAR 영상에서는 가우스 분포를 찾아보기 어렵다. 대부분 비대칭분포의 특성을 보인다.
그렇기 때문에 지금까지 익숙하게 사용했던 가우스분포보다는 감마분포(Gamma Distribution), F분포(F-Distribution), 레일리분포(Rayleigh Distribution), 카이제곱분포(Chai Square Distribution) 등과 같은 비대칭 분포에 친숙해져야한다.
그렇다면, 위에서 추정한 PDF가 어떤 분포를 보이는지 어떻게 알수 있을까?
선행연구에 따르면 우리가 사용한 Sentienl-1 GRD(Ground Range Detected)영상에서는 아무 물체가 없는 클러터 영역에서 픽셀이 감마분포를 따른다 (Canty, 2023).
파이썬의 scipy 모듈에서는 여러가지 통계적 분포를 분석할 수 있는 툴을 제공한다.
scipy 모듈을 이용해 수학적으로 계산된 감마분포를 추정하면 다음과 같다.
from scipy.stats import gamma
beta = np.var(sample)/np.mean(sample)
alpha = np.mean(sample)/beta
x = a[1][1::]
y = a[0]/sum(a[0])
plt.plot(x,y,'.', label='Data')
plt.plot(x, gamma.pdf(x, alpha, 0, beta)*(x[1]-x[0]), 'r-', label='Gamma Distribution')
plt.title('Estimated PDF')
plt.ylabel('Probability')
plt.xlabel('Sigma_naught')
plt.grid('on')
plt.legend()
plt.show()
위의 그림에서는 수학적으로 모델링된 감마분포와 실제 데이터를 비교해보면 높은 정확도로 일치하는 것을 알 수 있다.
그렇다면, 처음부터 수학적 모델을 사용할 수는 없었을까?
감마분포의 모양을 결정하는 alpha와 beta의 값은 실제 샘플링된 데이터를 통해 계산하여 파라미터를 추정해야한다.
SAR 영상은 같은 해양지역이라고 하더라도 국지적인 지역에 따라서 통계적 성질이 조금씩 바뀌기 때문에 샘플링은 필수적인 과정이다.
다음 포스팅에서는 모데링된 PDF를 이용해 통계적 가설검정을 수행하여 실질적으로 선박을 탐지하는 방법을 알아볼 예정이다.
Reference:
Canty. (2023). Detecting Changes in Sentinel-1 Imagery, Google Earth Engine | Google for Developers.
'인공위성과 지구통계학' 카테고리의 다른 글
| 지구통계학을 이용한 선박탐지(3)-통계적 가설검정 (0) | 2024.11.30 |
|---|---|
| Google Earth Enginge에서 위성영상 받아보기 (0) | 2024.11.30 |
| 지구통계학을 이용한 선박탐지(1)-SAR 영상 읽기 (1) | 2024.11.30 |